Inventing a New Type of Random Table

In expanding on the adventure nodes in yesterday’s post, I stumbled on an idea I’d like to explore.

This isn’t truly part of building the adventure, but it was sparked by an observation I had while doing so, so I’m considering it fair game for inclusion.

For now, I’ll refer to this idea as a ‘polarized table’. It can be used to generate results in a linear manner, or weighted toward one end or the other.

In an encounter table, you might have three zones: ‘easy’, ‘medium’, and ‘hard’. You create an encounter table with the weakest creatures in the lower-number slots, strongest in the higher-number slots, and the ‘average’ in the ‘middle’ slots. When it comes time to use it, you’ve got a few choices.

One of the simplest is to use different rolls on the tables. If you’re rolling for an encounter in the ‘easy’ area, you roll d12. In the ‘hard’ area, you roll d12+8. In the ‘medium’ area you might roll d10+5 (so you get mostly medium encounters, with a few of the ‘hardest of the easiest’ and the ‘easiest of the hardest’).

Slightly more work, you assign three different columns of ‘target numbers’, one for easy, medium, and hard. Or, as shown in the table below, ‘low-level spells’, ‘medium-level spells’, and ‘high-level spells’.

In both cases, you segregate the results by group (minor, medium, major, in this case). Each group is focused, but excludes a large amount of the table.

‘Polarized tables’ let you have potential access to the entire range of results, while keeping the focus on the region of interest. That is, with an encounter table you will much more likely encounter an ogre in the ‘easy area’ rather than a dragon, and vice-versa in the ‘hard area’.

It’s pretty simple: leverage the ‘advantage’ and ‘disadvantage’ mechanism. When rolling for an ‘easy encounter’, roll 2d20 and take the lower value. If you want a ‘hard encounter’, roll 2d20 and take the higher value. If you’re rolling for a ‘medium encounter’, either roll d20, or roll 3d20 and take the middle value (depending on whether you want ‘medium encounter’ to represent something from the middle rather than something from anywhere). You can scale it even further by rolling 3d20 and taking the lowest or highest as appropriate.

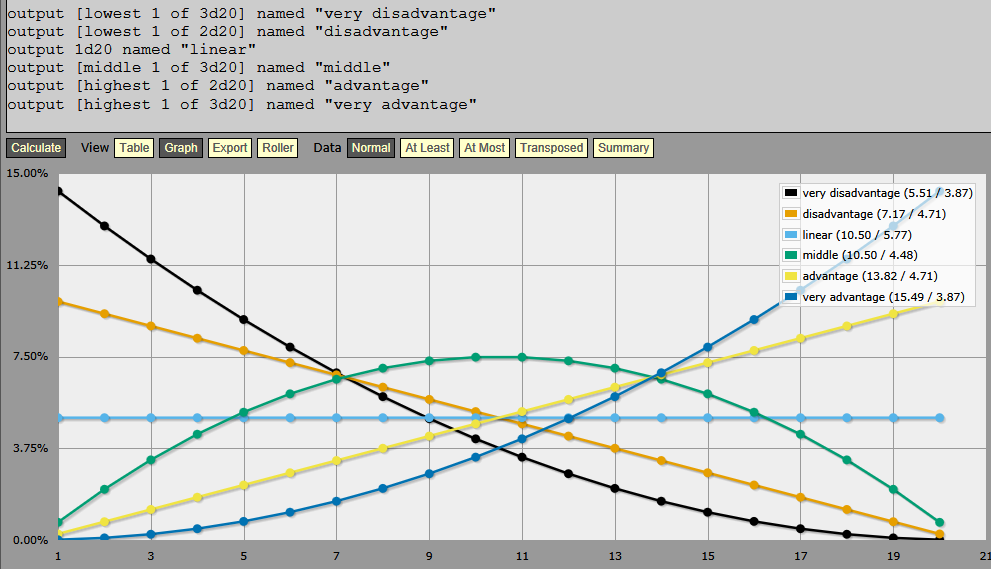
The table below shows the percentage chance of any particular result, when rolling ‘Very Disadvantaged’, ‘Disadvantaged’, ‘Linear’, ‘Middle’, ‘Advantaged’, and ‘Very Advantaged’

Result	V. Disad	Disad	Linear	Middle	Adv	V. Adv
	min(3d20)	min(2d20)	1d20	middle(3d20)	max(2d20)	max(3d20)
1	14.26	9.75	5	0.72	0.25	0.01
2	12.84	9.25	5	2.08	0.75	0.09
3	11.49	8.75	5	3.27	1.25	0.24
4	10.21	8.25	5	4.33	1.75	0.46
5	9.01	7.75	5	5.22	2.25	0.76
6	7.89	7.25	5	5.97	2.75	1.14
7	6.84	6.75	5	6.58	3.25	1.59
8	5.86	6.25	5	7.03	3.75	2.11
9	4.96	5.75	5	7.33	4.25	2.71
10	4.14	5.25	5	7.47	4.75	3.39
11	3.39	4.75	5	7.47	5.25	4.14
12	2.71	4.25	5	7.33	5.75	4.96
13	2.11	3.75	5	7.03	6.25	5.86
14	1.59	3.25	5	6.58	6.75	6.84
15	1.14	2.75	5	5.97	7.25	7.89
16	0.76	2.25	5	5.22	7.75	9.01
17	0.46	1.75	5	4.33	8.25	10.21
18	0.24	1.25	5	3.27	8.75	11.49
19	0.09	0.75	5	2.08	9.25	12.84
20	0.01	0.25	5	0.72	9.75	14.26

If you’re rolling for an encounter in the ‘easy area’, you’d roll ‘Disadvantaged’ or ‘Very Disadvantaged’: 2d20 or 3d20, taking the lowest. If rolling ‘Disad’ there is a 75% chance of ending up in the lower half of the table, if rolling ‘V. Disad’ there is an 87.5% chance of being in the lower half of the table. In both cases, though there is the possibility of getting a higher result. The highest result might be vanishingly infrequent — 1/8000 if rolling ‘very disadvantaged’ — but it’s not totally impossible, and while 0.25% is pretty unlikely it’s not totally unheard of.

I mean, we all managed roll at least one first-edition fighter with 18/00 Strength, right? 3d6 in order, swear to god.

The same pattern, simply reversed, happens at the upper end if you roll ‘Advantaged’ or ‘Very Advantaged’.

The linear result is self-explanatory, but I find the ‘middle’ result interesting.

Range	Frequency
10-11	14.94%
9-12	29.60%
8-13	43.66%
7-14	56.82%
6-15	68.76%

The remainder is divided evenly between lower and higher results. The middle six in the center — 8-13 differ by less than half a percent from least common to most common (7.03% to 7.47%). That’s as close to flat as I could care to ask, and the fourth entry (6 or 14) is still within 1% of the highest (6.58%).

Pictorially…

I used random encounters in this post as a simple case that required little additional  context, but there are other uses. Just about any time you might want three different zones in the same table, you could reasonably use polarized tables.

• Magic item selection (as shown above with minor/medium/major scrolls);
• Character traits, especially those already polarized (a lawful character might ‘roll disadvantage’ a table that could have ‘honest’ in a low-numbered slot and ‘deceptive’ in a high-numbered slot — it’s not impossible that a lawful character is deceptive, but many expect lawful characters are more likely to be honest).
  • This could be inverted: a character with the ‘honest’ trait might roll with disadvantage to see if he’s lawful or chaotic. He’s more likely to be lawful than chaotic, but you can’t rule it out.
  • It can even be extended: a character with no lawful or chaotic traits might roll 1d20, a character with one lawful and one chaotic trait might roll 3d20 and take the middle one, and one with two lawful traits and one chaotic trait might roll 4d20 and take the second lowest (discarding the two highest and the one lowest). I haven’t actually run numbers on that last option, though.
• Planar or energy traits: a plane of fire might roll on a fire-normal-water polarized table to see what it’s like. It’s not impossible for there to be a water-based trait there (though it’s unlikely… and probably short-lived or turns to steam), but it’s much more likely to be fire-based.
• Settlement traits: a lawful settlement could have some degree of corruption (possibly formalized, even), but you’re more likely to see corruption in a chaotic settlement (even if it has lots of rules).

I can see many places this might be useful. I’ll have to explore them.

Brief Addendum

I poked around a bit more with AnyDice and generated several more options, using increasing numbers of dice. I’m not entirely convinced it’s worth the extra trouble at the table, but it was worth the extra trouble to think about.

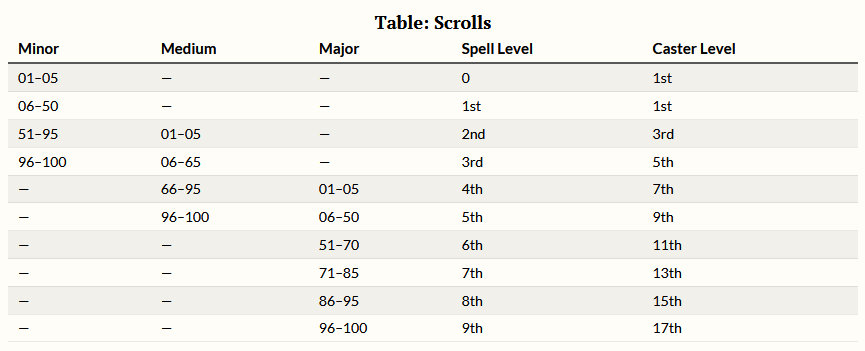
First, using 4d2: DDD (d20 with three disadvantage dice), ADD (d20 with one advantage die and two disadvantage dice), AAD, AAA.

This gives me a few focal points (of sorts) but I lose the middle one. Obviously five dice will fix that, but what does it look like?

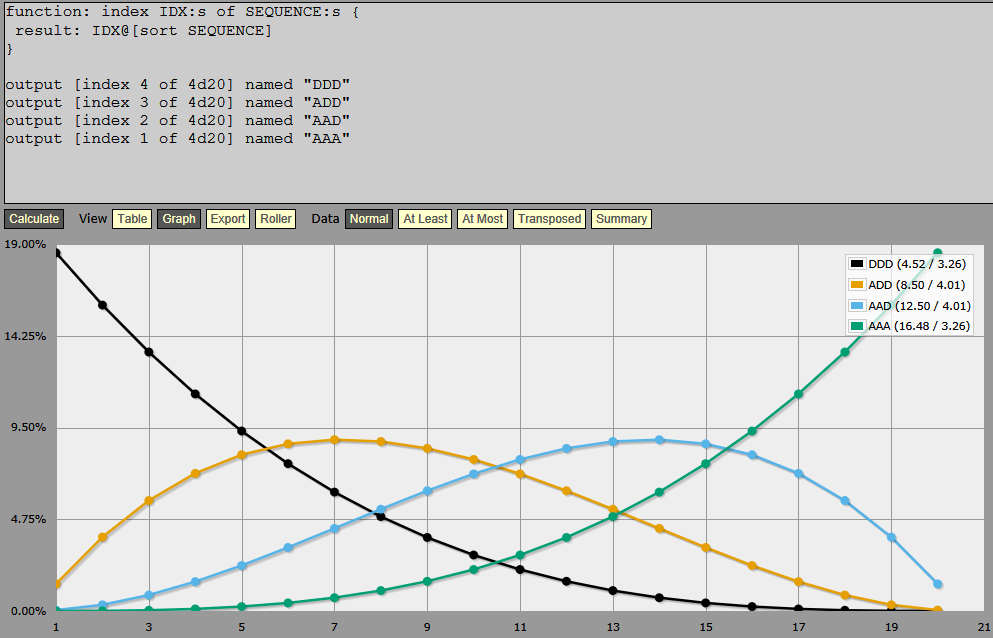
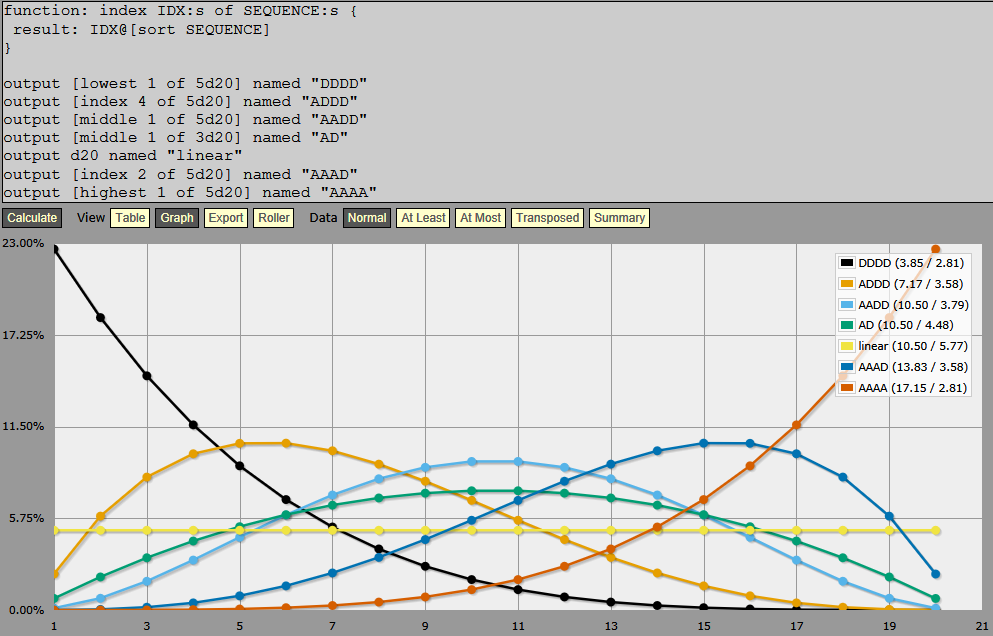
Busy, busy, busy diagram (seven lines!), but manageable because of the symmetry.

I think mathematically this has the characteristics I’m looking for. I have three focal points (about 5.5, 10.5, 15.5)  that are fairly flat near the focal point then drop pretty quickly to either side. I can still have outliers at either end, but even when I’m ‘in that region’ the odds of rolling the outlier (the weakest or strongest) is relatively small. Still several times higher than with some of the other rolls, but small enough that I can afford to put something that is more extreme than might otherwise be acceptable.

That is, I can probably afford to have ogres and dragons on the same table. The chance of getting one in the right region is small, the chance of getting one in the next region is even smaller, and the chance of getting one in the wrong region is vanishingly small. The most extreme formula (all disadvantage or all advantage) doesn’t do that, even when there are only two dice, let alone five (at which point you have a 23% of getting the lowest or highest value, depending which formula).

I’m just not sure I want to roll 5d20 when… actually, aw hell, 5d20 and select isn’t so much, I guess. Not when it gives me the opportunity to get results like this.