So I don’t forget, again… here are some notes about the syntax of a random table roller I wrote around 1997, 1998.
This random table roller was inspired by a random text generator I found in college called ‘BNF’. Data files for this program had a syntax based on Backus-Naur Form, a notation used for describing languages.
Enough history! That’s where this tool came from, but the syntax doesn’t look like that now!
Object Definitions
There are four object types in my random dictionary files.
Default Object
A dictionary file may have a single default object line.
!defaultSymbolExclamation mark and an object name, identifying the ‘table’ to resolve if no table is identified on the command line.
!SmallGods500When this dictionary is called without a named table, call SmallGods500.
Import Instruction
I’m a big fan of the DRY principle – Don’t Repeat Yourself. As such, I want to create tables once and reuse them when needed.
?filename.dictQuestion mark and the name of the file to import. All table and top-level symbol definitions in the imported file are added to the dictionary. Any default object in the import file is not imported. Imports can be nested (file A can import file B, and file B can import file C). Each file can be loaded once and only once; attempts to import again will be ignored.
?rsdn.dictLoad the file called rsdn.dict. This file has tables from Raging Swan’s Dungeon Dressing: Dungeon Names and Legends.
Variable Initialization
This engine is not strict. There is no need to explicitly declare variables, variables are created when found in the text.
Table Definition
This is the core content of the dictionary files. There are four line types involved. Not all are used in all tables.
&TableName [DefaultRoll]
< LowEntry
> HighEntry
|Weight TableEntry
|Weight TableEntry
|Weight TableEntryThe table structure is pretty straightforward, I think. There is no particular order needed, after the table declaration. By convention I like to put the LowEntry and HighEntry at the top because they are rarely used. I want to them to stand out and be easy to find.
- TableName is, of course, the name of the table. By convention I use alphanumberunder (letters, digits, and underscores), but I’m pretty sure the only restriction is ‘no whitespace’. Strong convention; I’ve never tried hyphens and the like.
- DefaultRoll is the roll to apply when using the table. This is optional; if you don’t specify, the default roll will be ‘d(sum(weight))’. That is, if the weight of all entries is 20, the table will use d20 unless you say otherwise.
- LowEntry is used when the random roll is less than 1.
- HighEntry is used when the random roll is greater than the cumulative weight of the entries.
- Weight is the number of roll results that will cause this entry to be chosen. When rolling on a table with a d20, a weight of 1 gives a 5% chance of getting that entry. If the roll uses multiple dice (d8+d12, like AD&D2e random encounter tables) the percentages will not be linear.
- TableEntry is the content that will applied when the entry is chosen.
LowEntry, HighEntry, and TableEntry all use the same syntax when resolving. I’ll describe that in a section below.
&SmallGods500
|1 @iter{&toadSmallGod}{500}{\n}\n
&toadSmallGod
|1 &toadSmallGodName, &toadSmallGodEpithet
&toadSmallGodName
|5 &toadSmallGodName2
|3 &toadSmallGodName3
|1 &toadSmallGodName2 &toadSmallGodName2
|4 &rsdnProperName
|2 &rsdnProperNamePrefix-&rsdnProperName
&toadSmallGodEpithet
|1 &toadSmallGodEpithetA &toadSmallGodEpithetBThis is only four of the ten tables in this file (toadSmallGods.dict). rsdn.dict has 156 tables, with an average of about 10 entries.
Ignored Lines
Blank lines, and lines starting with a hash character (‘#’) are ignored by the engine and skipped.
Entry Syntax
The structure above is all about containing table entries. Each entry starts with the selection criteria (low, high, or weighted), white space, then the entry content. The white space is ignored. To have a space at the start of an entry’s text, escape with a backslash (‘\’). The entry then has some number of these segments.
- Static text. This is the default, unless a special character indicates otherwise.
- Variable assignment.
=variable{value}assigns ‘value’ to ‘variable’. Value will be resolved as other text. This also will be output as text. - Variable output.
$variableoutputs the value of ‘variable’. - Calculation.
%{formula}calculates the value of ‘formula’. This can involve normal numbers and operators, dice expressions such as ‘3d6’, and variables - Function call.
@function{parameter}calls the named function, passing the parameter. A function may have any number of parameters. Functions are all defined in code, I’ll list them below. - Table call.
&tablecalls the named table, using the (implicit or explicit) default roll.&table{roll}calls the named table, using the specified roll. This ‘roll’ is resolved as for the calculation above: variables, static numbers, dice expression, formula. Resolving a table assigns the value rolled to a variable with the same name as the table.&gemSizecalls the ‘gemSize’ table, and stores the roll result in$gemSize. - Masked.
`expression`will resolve the expression, without outputting text. - Escaped. Special characters above can be output as text by prefixing them with a backslash (‘\’). There are some other escape sequences, described below.
This is not a fully-functional language, but it does cover a fair bit of ground.
Functions
The function list isn’t very long. In alphabetical order…
@an{param}prefixes param with'an 'if param starts with a vowel, or'a 'if not. Vowel is defined here as[AEIOUaeiou];[yY]are rarely ‘vowels’ when they start a word.@cap{param}makes the first character of param an uppercase letter, if it is a lowercase letter.@if{test}{pass}{fail}resolves test. If test is not 0, it resolves and outputs test, otherwise it resolves and outputs fail.@if{test}{pass}also works (implicitly ‘fail’ is the empty string).@iter{param}{iterations}{separator}iterates iterations times. Each time it resolves and outputs param, and separates the iterations with separator.@iter{&Gem}{100}{\n\n}\ncalls the Gem table 100 times, separating the outputs with two newlines. Then appends a newline at the end of the entire output.
@mod{roll}{denom}gives the modulus of roll and denom. This is like the % operator in C/C++/C#. If denom is0,@modreturns0.@mod{5}{3}returns2.
@plural{param}{count}and@plural{param}{count}{pluralval}make param plural form when count is not equal to 1. If called with the third parameter,@pluralreturns pluralval, else it returns param with an ‘s’ appended.@roll{param}resolves the value of param. This is the same as the ‘%’ operator.@uncap{param}makes the first character of param a lowercase letter, if it is an uppercase letter.
Comparison Operators
Comparison operators all take the form @function{left}{right}{pass}{fail}. The function resolves left and right and compares them as numbers. If the test passes, the function outputs pass, otherwise it outputs fail. as with @if{}, fail can be implied.
@eq{left}{right}{pass}{fail}returns pass if left equals right, else fail.@ge{left}{right}{pass}{fail}returns pass if left is greater than or equal to right, else fail.@gt{left}{right}{pass}{fail}returns pass if left is greater than right, else fail.@le{left}{right}{pass}{fail}returns pass if left is less than or equal to right, else fail.@lt{left}{right}{pass}{fail}returns pass if left is less than right, else fail.
Table Manipulation Operators
A few days ago I integrated some operators from Seventh Sanctum. I added a backup member to Dictionary, holding all the tables as originally loaded. Then I added functions to manipulate the tables member (which is used during resolution).
@appendTable{target}{source}appends the source table to the target table (drawn fromtables, notbackup).@resetTable{target}resets the target table to the original form (copies frombackup).@replaceTable{target}{source}replaces the target table with the source table (drawn fromtables, notbackup).@addEntry{target}{weight}{entry}{mask}adds entry to the end of target with a weight of weight (and optionally, a mask of mask). Mask is not mandatory; if not present it defaults toMASK_ALL.- When added, entry is treated as raw text and not resolved. You can add
&callTableand it will add the instruction to call callTable.
- When added, entry is treated as raw text and not resolved. You can add
@addResolved{target}{weight}{entry}{mask}works as addEntry, except entry is resolved. That is, in the example above,&callTablewould in fact call callTable and store the result.@removeEntry{target}{roll}removes the entry from target that would be chosen if roll was used as input. If roll is 0 the LowEntry is removed, if roll is greater than the the table’s weight, HighEntry is removed.- This does not respect masks. When resolving a masked call a new table is created, used, then discarded.
Escape Codes
Sometimes, you need to output a special character. There aren’t many, but they’re important.
- \n is a newline.
- \t is a tab.
- \s and ‘\ ‘ (backslash followed by space) is a space. This is really useful only at the start of an entry.
- \ at the end of a line is a continuation marker
- \ followed by any other character outputs that character. This is most often useful with @, $,,%, &, =, `, and \.
Not many, but useful.
Dice/Math Expressions
Math expressions work as you would expect: BEDMAS applies as expected, except with no exponents.
There are a few things not common in normal math, though.
- Variables as defined above are respected.
- Dice expressions matching
NdMsyntax (N is implicitly 1 if not present) work as expected.- I say that, not expecting the N or M to be non-numeric. That is, you can’t do something like “10d$dieSize”.
- You can, however, do “4d6d10”, which will resolve as “4..24 d10s”.
Only the normal arithmetic operators work. No exponents and only the @mod function to expand on that.
Sample File: gemJewelry.dict Excerpt
I wrote this dictionary file about 30 years ago, based on an article from Dragon Magazine (“Just give me MONEY!”, issue 167).
!GemsDefault
$iter 10
$table Gem
&GemsDefault
|1 \n@iter{&Gem}{$iter}{\n\n}\n
&j
|1 `=iter{100}`\n@iter{&Jewelry}{$iter}{\n\n}\n
&Gem
|1 @cap{@an{&gemSize}} &gemType (base value $gemBase cp)\n\
quality\t&gemQuality ($gemQuality\%)\n\
size\t$gemWt pennyweight\t(%{$gemWt*25}\%)\n\
`=gemValue{%{$gemBase*$gemWt*$gemQuality/400}}`\
value\t&Value{$gemValue} ($gemValue cp)The first line says to call GemsDefault as the default table.
The third and fourth lines set the $iter and $table variables (though $table never gets used).
&GemsDefault has only a single entry, which does several things.
- Outputs a newline.
- Makes
$iter(10) calls to the&Gemtable, separating each pair with two newlines. - Ends with another newline.
The &Gem table also has only a single entry, outputting a string that looks something like
An average fire agate (base value 400 cp)
quality normal (100%)
size 4 pennyweight (100%)
value 1 gp (400 cp)
A large amethyst (base value 4000 cp)
quality normal (100%)
size 10 pennyweight (250%)
value 25 gp (10000 cp)The entry has these elements.
- First line
@cap{@an{&gemSize}}calls thegemSizetable, which returns a descriptive size (and stores a pennyweight value).&gemTypecalls thegemTypetable, returning a named gemstone and storing thegemBasevalue.- Static text ‘ (base value ‘.
- Outputs the cp value stored in
gemBase. - Static text ‘ cp)’ + newline.
- Continuation marker.
- Second line
- Static text ‘quality’ + tab.
- Calls
gemQualitytable to get a descriptive gem quality, and stores a gem quality coefficient in$gemQuality. - Static text ‘ (‘
- Quality coefficient stored in
$gemQuality. [Note that this contradicts the implicit ‘store die roll in variable with same name as table.] - Static text ‘\%)’ + newline [with the ‘%’ escaped with a backslash).
- Continuation marker.
- Third line
- Static text ‘size’ + tab.
- Pennyweight value stored in
$gemWt. - Static text ‘ pennyweight’ + tab + ‘(‘
%{$gemWt*25}multiplies$gemWtby 25 and outputs the result- Static text ‘\%)’ + newline [‘%’ escaped]
- Continuation marker.
- Fourth line
- ‘secret’ assignment to $gemValue: gemBase * gemWt * gemQuality / 400 (calculates and stores with no output).
- Continuation marker.
- Fifth line
- Static text ‘value’ + tab
- Calls the
Value“table” to format the value of the gem, passing $gemValue as the input. - Static text ‘ (‘.
- Outputs the raw $gemValue (cp value).
- static text ‘ cp)’
This is an unusually complex entry, with a lot going on. I think it hit all the high points, though.
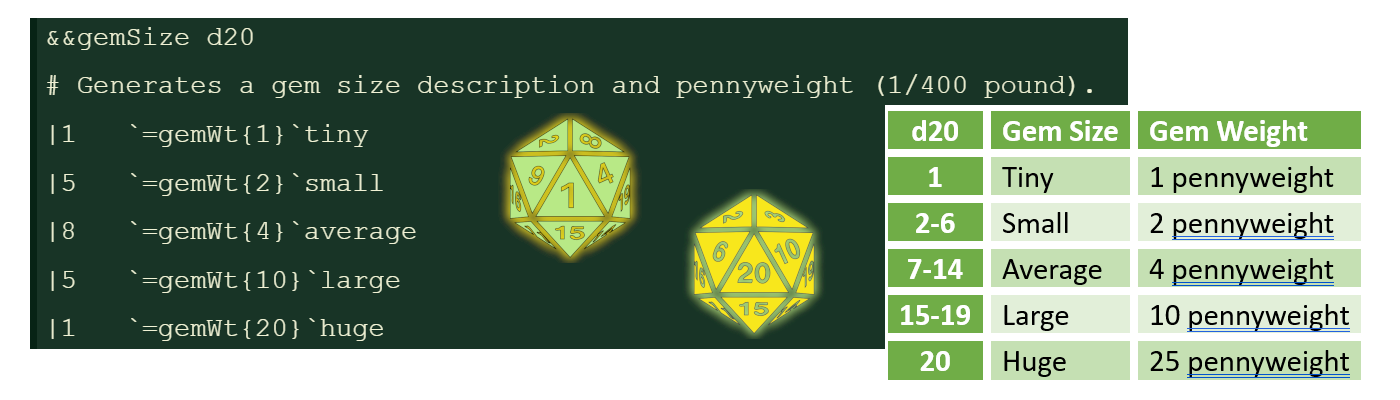
&gemSize d20
< `=gemWt{1}`tiny
> `=gemWt{25}`huge
|1 `=gemWt{1}`tiny
|5 `=gemWt{2}`small
|8 `=gemWt{4}`average
|5 `=gemWt{10}`large
|1 `=gemWt{20}`hugeA much simpler example. This one includes a default roll (that matches the aggregate weight; it’s redundant).
Each entry assigns a value to gemWt, being the pennyweight (1/400 of a pound) of the gem. If the caller to this table provides a roll that goes outside 1..20, the gem will be 1 or 25 pennyweight.
&gemType
|11 `=gemBase{400}`&gemOrnamental` [ornamental]`
|4 `=gemBase{2000}`&gemSemiprecious` [semi-precious]`
|2 `=gemBase{4000}`&gemFancy` [fancy]`
|2 `=gemBase{20000}`&gemPrecious` [precious]`
|1 `=gemBase{40000}`&gemGem` [gem]`
> `=gemBase{200000}`&gemJewel` [jewel]`As with gemSize, but assigning a base gem value to gemBase. There also is a secret static string “[description]”. This was originally part of the output, but I used ‘secrets’ to hide it from view. I didn’t want to show them, but I didn’t want to delete them, either.
&Value
|39 $Value cp
|360 %{$Value/40} sp`=rem{@mod{$Value}{40}}`@if{$rem}{, $rem cp}
> %{$Value/400} gp`=rem{%{@mod{$Value}{400}/40}}`@if{$rem}{, $rem sp}This is the last example for tonight. I used the table mechanism to create a function, of a sort. It takes the input value and converts it to two-denomination resolution. The Dragon article this dictionary was based on used 10 sp = 1 gp and 40 cp = 1 sp.
- If the value is less than 40 cp (i.e. less than 1 sp), output ‘
$Valuecp’. - If the value is 40..399 cp (less than 1 gp), output ‘
$Value/40sp’ (division truncates), then assign the remainder to$rem. If this is not zero, output ‘,$remcp’. - If the value is 400 cp or more, do the same but for gold and silver. Divide by 400 to get the number of gp, then take the remainder and divide by 40 to get the sp. Output accordingly.
Closing Comments
This post took a lot longer than I anticipated, but I think it was worth it. I’ve never taken the time to write this, so it’s good to finally have it documented.