While working on Icons in the Sandbox, though, I realized a limitation in the polyhedral process that doesn’t much come up when creating pantheons.
Even if there are multiple pantheons in a campaign setting, even if those pantheons interact, you can pretty reasonably create each on its own polyhedron and simply throw the results together. You can even do that within a single pantheon, as with the Æsir and Vanir of Norse mythology.
It seems more difficult with icons, though. If I just want to increase the number of icons I can do much as I might with deities, creating a new roster… but I have the sense I’d want to instead expand the set while maintaining some of the same members and coherence in trait assignment.
That is, in the Icons in the Sandbox series, the Radiant Lady and the Exemplar both are from a foreign land, interested in bringing ‘civilization’ to the island. Perhaps they aren’t totally in step with each other, each having their own agenda, but they are both here and working for the glory of the Empire. The Hound also is here, but is no longer so trusted by her former comrades.
Regardless, all three are from somewhere else. While it’s entirely possible they were exiled here and lack power in their homeland, I’m going to assume they either held power before or have become significant because of their activities here.
As such, it seems to me they could be treated as icons in their homeland as well, and there should be others who are not so relevant on the island but are considered icons in their homeland.
So… how can I expand my roster of icons in a way that retains coherence similar to the original set?
Intersecting Polyhedra
In the example here, I’ve got icons who are relevant in two regions. The simplest way to do this is to simply start a new polyhedron with the shared icons (and their traits), then assign new traits to the other sites on the new polyhedron and define new icons.
I’d originally expected to bring all three icons with the ‘civilized’ trait over, but since the Hound was ‘only’ an officer and her power is centered on the island rather than in the Empire, I’ll leave her out.
I copied the Radiant Lady and the Exemplar, and their traits, to a new icosahedron. This means I keep the following eight traits, but have twelve more that are unassigned.
- Craft/Artifice
- Civilization
- Raid
- Church
- Animal
- Glory
- Quest
- Sun/Moon
Of the icons, though, I have:
- Radiant Lady (as she was on the island)
- Exemplar (as he was on the island)
- two new icons that share three traits with icons on the island (two new traits)
- four new icons that share two traits with icons on the island (three new traits)
- four new icons that share no traits with icons on the island (five new traits)
It seems like this could have a fair amount of coherence with the first sandbox, while having plenty of room for new icons that are significantly different.
Tessellated Shapes
In the absence of a better name… one of the ideas GreyKnight (or possibly Barry Payne of Sycarion Diversions) had years ago was to flatten the polyhedron into a plane. This can be extended indefinitely, which gives lots of room for development.
On the other hand, while it’s possible to tesselate many shapes, the three simplest ones (squares, hexagons, and equilateral triangles) are… uninspiring. Workable, but the sheer regularity of the shape doesn’t feel great to me.
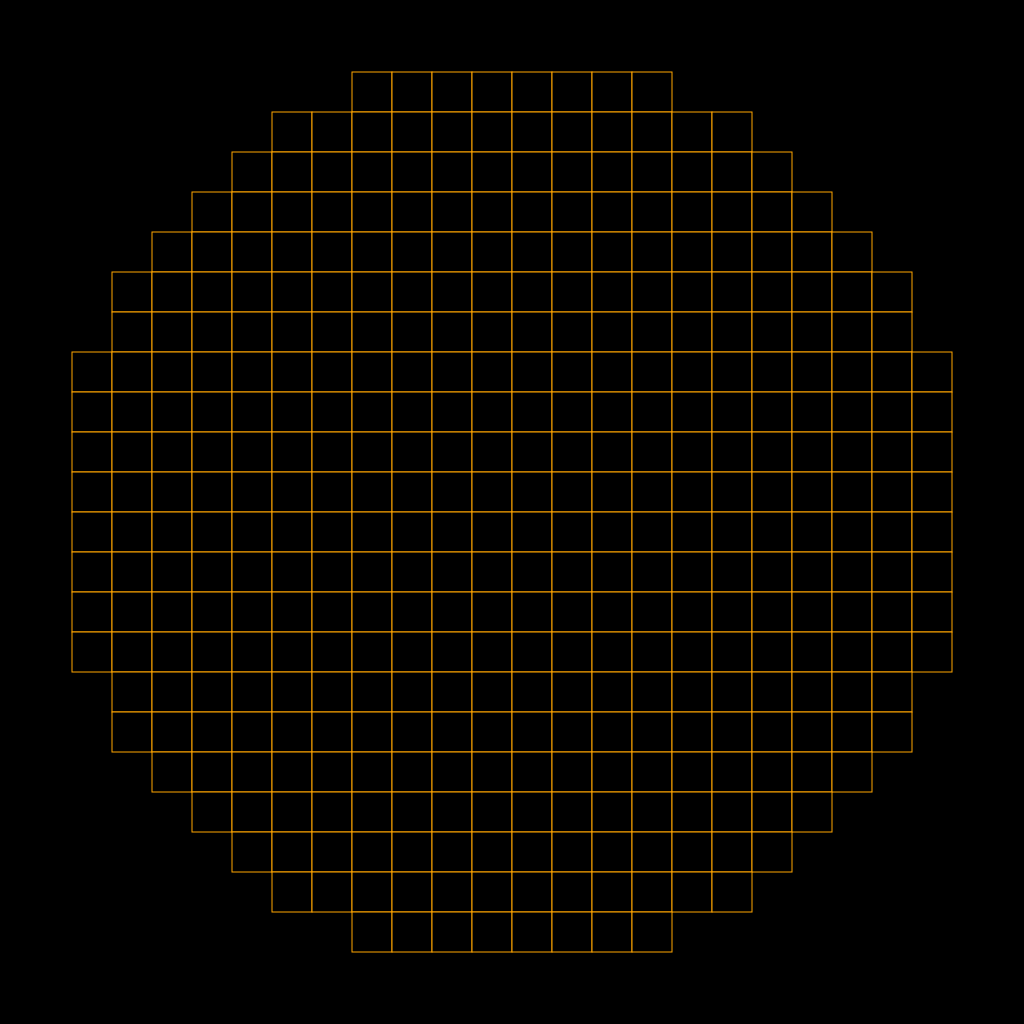
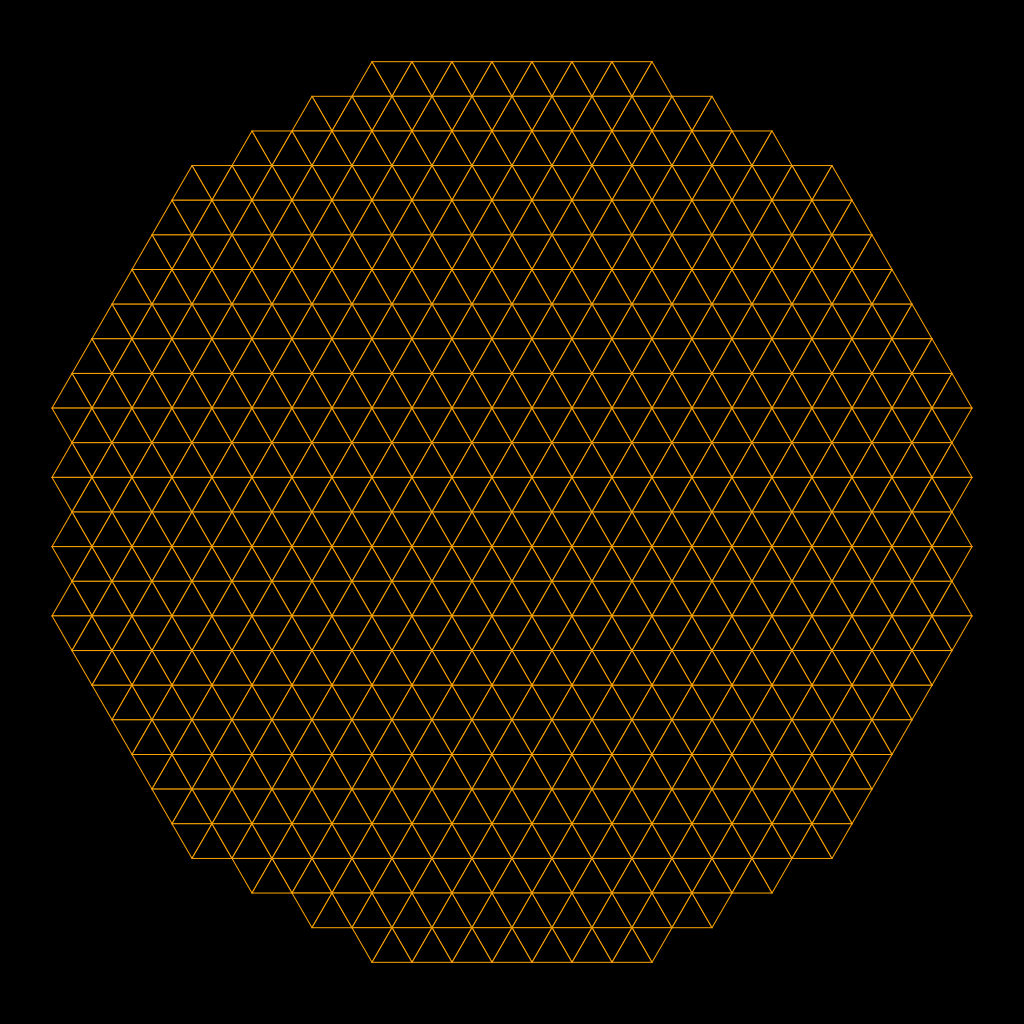
Still, ‘simple and works’ does have a lot to go for it.
On the other hand… Kublai (Random Wyvern Publishing) reminded me of Penrose tiling. Investigated and described by Roger Penrose, these are aperiodic (i.e. no repeating patterns) but has some very useful characteristics for my purpose.

Depending how I assign the traits and determine the icons, I get:
- Equilateral Triangle plane:
- Assigning traits to faces, and icons to points, each trait applies to three icons and each icon has six traits.
- Assigning traits to points and icons to faces, each trait applies to six icons and each icon has three traits.
- Of the two, I prefer assigning traits to faces. If I really want more icons a particular trait I can assign it to multiple faces, and having only three traits per icon seems like they would be less differentiated that I’d want.
- Easy to implement. Define an origin and a mapping algorithm based on row and column (this can trivially be reframed to fit a cartesian-like coordinate system).
- Hexagon plane (not shown above):
- This is functionally the dual of the equilateral plane, so for me it’s the same thing.
- Still easy to implement; perhaps not as trivially reframed to fit cartesian-like coordinates but since it’s the ‘dual’ of the equilateral plane it can be done.
- Square plane:
- Whether I apply traits to points or to faces, and icons to the other, I end up with each trait applying to four icons and each icon having four traits. Workable but I’m not excited.
- Trivial to implement, I could probably do it in a spreadsheet without too much difficulty (if we ignore the ability to arbitrarily increase size).
- Penrose plane:
- All faces in the picture above are quadrilaterals. If I assign traits to faces then each trait applies to four icons, and if I assign traits to points each icon has four traits.
- Points connect to different numbers of faces. I see points touching three faces, five faces, and in some uncommon cases, seven faces. This means if I assign traits to faces I could end up with icons with three, five, or seven traits, and if I assign traits to points I could end up with traits shared between three, five, or seven icons.
- I don’t even know where to start implementing this one. It can be done manually if you have a big enough paper with a Penrose tiling drawn on it, but using it would be more work than I care to do. I’d want software, but writing this at 12:30 AM I lack the imagination to figure out how.
Of course the one that will be hardest to implement is the one that most interests me.
Closing Comments
I’ve wanted to explore this topic for quite some time. I’m happy to see I’ve got some options to explore.
- Intersecting Polyhedra will be trivial to implement. Assuming you use the workbook that ships with Polyhedral Pantheons, just take a copy of the relevant worksheet, reset the icons you don’t want and the traits not used by the icons you do want, then fill in new traits and new icons.
- Regular tessellations — equilateral triangle, hex, and square — are fairly straightforward to implement. I don’t have the tools at the moment, but they wouldn’t be hard to figure out.
- Penrose tiling fascinates me, and has several characteristics that really appeal to me, but I really don’t see yet how I could implement this in a workable way. But I’m willing to take a run at it.
With that, time to sign off.