When building a scenario or other campaign entity, I like to graphs to show in an abstract way how various things link to each other. Sometimes I like to build purely organically, constructing these graphs as I think of the entities, but lately I’ve been taking a page from the eurogames design pattern — build the structure first, then fill in the content. That makes it somewhat easier to prove that everything works, but does have the risk of being ‘overly patterned’ or repetitious in structure.
I want to draw the graphs first, but I want them to simultaneously be uneven enough to be interesting while still having enough linkages and structure to get the job done. If they can be drawn as planarities (no edges crossing), so much the better. This rules out a lot of purely random approaches, but I think I found something that will give me what I’m looking for.
I used to read a lot of Piers Anthony when I was a kid. In one story, I believe it was called Macroscope, there were a bunch of scientists who liked to play a sort of puzzle game called ‘Sprouts’.
The game starts with some number of dots on a piece of paper. Each player takes a turn drawing a line between two dots, and adding another dot on that line. A line may only be drawn between two dots if it does not cross another line, and neither dot has three lines touching it. Play continues until no more lines can be drawn, and the last person to play wins.
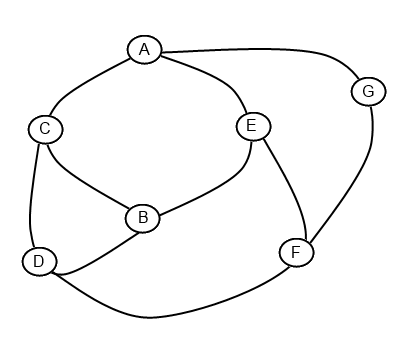
Incidentally, drawing one of these games on the computer is a pain and probably more trouble than it’s worth, but it’s pretty quick and easy to do with pen and paper. The image to the right is a representation of the ‘game’ I played for this post. Nodes A and B are the original two nodes, the rest were added in the order indicated by their letters (C, D, E, F, G in order).
I did an analysis because at one point I thought the winner might always be predicted from the number of dots. The maximum number of dots in the planar graph can be predicted from the number of starting dots (I haven’t worked out the exact formula), but it turns out the results can unpredictable if players strand (isolate) dots so no new lines can reach them.
I recently realized that this could lend itself well the node-base scenario structure I use.
Given a game starting with two dots, I ended up with a set of seven nodes, as shown to the right. I redrew the graph using GraphViz because my scribbles tend to be kind of unsightly. Letter assignments are arbitrary, and in fact I think it best that it be possible to enter the structure via several of the nodes. That ‘A’ is shown at the top and is the first letter in the alphabet should be no indication that it is ‘the way in’. I will admit that it is likely a way in, but many other nodes may provide access to the scenario structure.
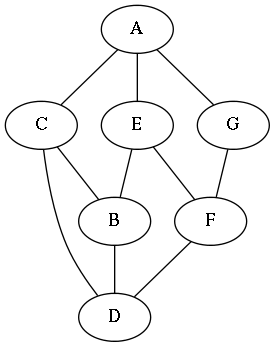
This is a fairly small graph, probably suitable for a scenario possibly involving a small number of scenes or locations. Assuming the edges are bidirectional and sufficient to move between nodes, it is possible to get from node A to any other node in no more than two steps. In fact, you can get from any node to any other node in no more than two steps except between nodes G and B.
While there are only seven nodes to this graph, I believe it has a lot of potential as the core of a scenario structure.
Each of these nodes can be broken down further, much as I did for the Node-Based Megadungeon (each colored region on the big graph was a single node in the original graph) — the eleven original nodes became somewhat over one hundred by the time I was done, and many of those could have been further broken down to describe the areas. For instance, in the Clockwork Hell many of the areas could reasonably consist of several rooms or smaller structures. It isn’t always worth doing this; the Goblin Warren and the Wolf Den both have areas that are fairly simple and probably don’t need much expansion.
It is also possible to add edges and nodes to this. Nodes B or E look like they would make good transit hubs. Simply adding a edge from B to F or E to G would make it so travel between any two nodes in the graph will require no more than two steps, assuming no obstructions or unidirectional edges.
The graph shown here might also describe only the core structure of the scenario. Each node (except G) is fairly well-connected, with three edges in or out. According to the Rule of Three it should be pretty easy for the players to be able to make reasoned decisions about the direction of travel. For example, from node B you can move to nodes C, D, and E directly. Enough information should be made available that the choice of direction is reasoned.
Depending on the scenario it may well be reasonable that each significantly different hook into the scenario links to a different node. If node A represents a murder scene, node F might be something important about a specific magic item. If the PCs are searching for that magic item, or needed to talk to the victim (or accused!) at A, you have two potential hooks into the scenario that can send the story in rather different directions, depending what happened. The PCs might be tangled into the murder and find out it was about the magic item, or might be seeking the magic item and find out there is a related murder (and solving that might let them find out who has the magic item).
That was a simple graph, such as might be appropriate for scenario or short set of scenarios (I view these things fractally; just as a scenario is constructed of encounters and scenes, a campaign might be constructed of scenarios).
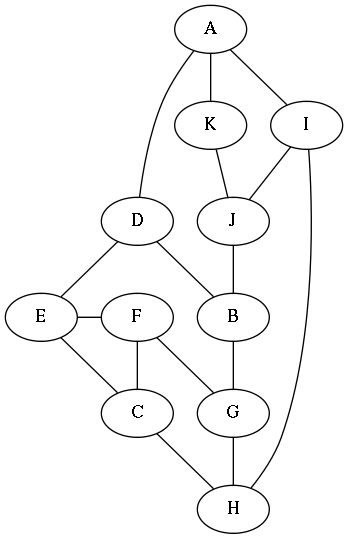
Larger graphs are possible, simply by starting with more ‘dots’. The graph shown to the right started from three dots and has eleven nodes. As with the previous graph the size is a little deceptive. It is possible to move between any two nodes in three steps or less except nodes F and K (minimum four nodes).
I might use this for a megadungeon (the Node-Based Megadungeon started with eleven nodes, but more variation in the number of edges, from two to four). It could also make a good, smallish sandbox, or be used to flesh out a node in a larger, more encompassing sandbox. I think at this size it’s starting to get a little too large to make a good scenario for me to run because there may be too many things to keep track of.
Adding an edge between nodes D and F would make it possible to move between any two nodes in no more than three steps.
It is possible to expand on the edges as well. I mostly avoid linear elements in my design, but treating an edge as an ‘implied node’ gives some freedom for more linear challenges. These might be something like a tunnel where there are multiple places where something must be done, or a mountain pass with similar characteristics, or maybe some place with defense in depth, where you must overcome the challenge to reach your goal.
I don’t imagine I would make use of it very often. I rarely find linear elements to be very interesting and they limit player agency (“go forward or back?” are pretty boring choices)… but if linear elements must be present, these might be good places for them.
I’ve drawn some larger graphs using more ‘dots’ to start, but I find they don’t really add much. It’s pretty easy to end up with a graph that’s basically split in two (parallel series of nodes, rather than interacting series of nodes). I find that seven nodes is a pretty comfortable number to work with, and eleven is about as many as I want to try to remember at any given level, so starting with two or three dots is about right. Starting with one dot still gives three nodes in a really boring graph, so I don’t imagine I’ll use that one much.
This will likely work better by starting with either a two-dot or three-dot graph (such as I’ve shown here, though new ones can be created). From there, expand on and create a new graph for each node as needed and link those together. Add or remove edges as needed, and even new nodes where you want.
I think this will provide a reasonable means for generating new graphs of manageable size and interesting complexity. Almost all nodes have enough edges to provide a good range of choice to the players, without it all becoming overwhelming.
Oh man. I completely forgot to mention that this works not only for scenario design and campaign design (linking scenarios), but it also works for other game entities such as organizations. I suppose I now have an idea of what I’m writing next.
The game from Macroscope is called “sprouts”, there is an entry for it in Wikipedia.
Well spotted, Winchell. Thank you.
I didn’t realize there was so much to it. The game is quite simple, there are people investing serious time analyzing it.
The Wikipedia article on Sprouts can be found at http://en.wikipedia.org/wiki/Sprouts_(game).
You seem to be assuming all connections are bidirectional. I suppose this is true in a lot of cases, but I suspect it’s not always true. If the graph represents a dungeon, one connection might be “take this 1-way teleport” or “trip a wall-closing trap behind you”.
If it’s a representation of a scenario — I’m not sure what bidirectionality means. A has a clue that leads to B, and vice versa?
It is not necessary that an edge by bidirectional, though I expect that often they will be. As you say, there can be one-way teleporters or other methods that are unidirectional. Or only currently unidirectional — at one point a trip down the waterfall might be a one-way journey, but after you learn fly you might be able to come back up that way.
If the graph represents physical locations, I expect that the edges will most often be bidirectional because presumably things live here. Even when the edges are not bidirectional it will be possible to get from any node to any other node by some path or another, if only because you want it to be possible. If the PCs cannot get to a place there is no practical purpose to it being there.
Some edges might not be accessible when first found. There might be a broken bridge that requires repair, or barriers that must be removed (locked doors, or even closing off a waterway that is flooding the passage you need to use). I know that Zelda games do this a fair bit, where getting to a place the first time is a long and troublesome journey, but part of the reward for doing so is opening an easier or shorter path (in at least one case the exact example I mentioned — fixing a bridge).
As for a scenario, there may also be bidirectional or unidirectional edges. In the Node-Based Megadungeon you can find dwarves at the Safehold talking about things seen in the Clockwork Hell, and at the Clockwork Hell you can find dwarves working on and studying the place. On the other hand, you might not see any sign of Aristothanes in the Clockwork Hell, but when you visit Aristothanes’ Sanctum you will likely find information pointing back to the Clockwork Hell.
I think a mystery-style scenario might be similar. In fact, it might work pretty well with bidirectional clues, since ultimately everything is related (except the things that aren’t, of course). In each place you might find one or more clues, plus hints of one or more other places to look. From what I’ve read of such stories the protagonist often discovers an edge of the situation and has to worry at it for a while to shake more pieces loose, until he has enough to figure out what’s going on. I suspect it’s entirely reasonable for edges in a mystery scenario to be bidirectional.
It might take a bit of practice, though. I don’t do a lot of mysteries, I’ve rarely had players that were interested in them.